GSL科学计算库、随机变量的Erlang分布与Weibull分布

Tue, 17 May 2011 11:08:30 +0800

更新：本文升级版“GSL科学计算库、随机变量的Erlang分布与Weibull分布”已经迁移至我的新博客http://gnailuy.com/。新文章对已有内容做了修改，并新增关于Weibull分布的内容。欢迎猛击这里：传送门。

=====旧文：=====

本文介绍了GSL库和Erlang分布的一般知识，以及使用GSL库生成服从Erlang分布的随机数的方法。对计算机生成的随机数，可以有许多算法对它们进行测试，例如一个常见的测试是Kolmogorov-Smirnov测试，也称作K-S Test。云师姐的这篇文章有使用Matlab进行KS-test的示例以及代码。

GSL及生成随机数的一般方法

GSL(GNU Scientific Library)是GNU组织的数值计算C/C++函数库。它是自由软件，依从GPL协议发布。GSL提供了大量关于数学计算的函数库，当然也包括本文用到的随机数生成函数。更多关于GSL的信息可以到GSL的主页去了解。

计算机中产生服从各种分布的随机数，其基础是产生服从均匀分布的随机数。得到服从均匀分布的随机数以后，可以通过许多不同的算法产生服从其他分布的随机数，例如较常见的使用Polar(Box-Mueller)方法(gsl-1.9/randlist/gauss.c中函数gsl_rand_gaussian)或者使用Ziggurat方法(gsl-1.9/randlist/gausszig.c中函数gsl_rand_gaussian_ziggurat)产生Gaussian分布的随机数等(参考William H.Press等人的著作《C数值算法》)。

服从均匀分布的随机数亦可由许多不同的随机数生成器来产生，不同的随机数生成器生成随机数的速度、随机性等均有差别。GSL库提供了12种随机数生成器(来源)。其中速度最快的是taus、gfsr4和mt19937(default)这三个生成器，而随机性最好的则是ranlux系列算法，也就是GSL的ranlxs系列生成器(来源)。ranlxs系列生成器中，ranlxs0、ranlxs1和ranlxs2产生24位单精度随机数，ranlxd1和ranlxd2产生48位双精度随机数。这五个生成器名字后面的数字代表luxury的程度不同，较高luxury程度的生成器产生的样本数据之间相关程度较低。值得一提的是，计算机中这种使用确定算法产生的所谓随机数，都是伪随机数(参考Knuth的《计算机程序设计艺术》卷二)。然而上述产生伪随机数的生成器由于具其生成的数据具有一定的随机性而得到了广泛的应用。

使用GSL库生成随机数的一般方法如下：

一、创建一个随机数生成器实例

?
创建随机数生成器实例
1
r = gsl_rng_alloc(T);

这里的T是gsl_rng_type类型的指针，它可以是gsl_rng_default(即gsl_rng_mt19937)、gsl_rng_ranlxs0或者gsl_rng_ranlxd1等，用于指定使用不同的随机数生成器。

二、生成种子

?
产生种子
1
gsl_rng_default_seed = ((unsigned long)(time(NULL)));

同一般我们使用C语言中的srand和rand函数一样，通常我们采用当前时间作为种子，以提高随机性。

三、生成服从指定分布的随机数

?
生成随机数例子
1
2
3
4
5
6
7
8
9
for (i=0; i<n; i++)
{
    u = gsl_rng_uniform(r);
}
 
for (i=0; i<n; i++)
{
    u = gsl_ran_erlang(r, erlang_a, erlang_n);
}

这里可以使用GSL提供的一系列函数生成服从各种不同分布的随机数，例如上述代码生成n个服从Uniform分布的随机数和n个服从Erlang分布的随机数，其中参数r就是上述生成的随机数生成器实例的指针，其他参数将在后面解释。

四、释放随机数生成器

?
释放随机数生成器
1
gsl_rng_free(r);

类似于C中的malloc和free函数，这里的随机数生成器实例也需要进行释放，避免内存泄漏。

在Linux下使用GSL库很容易，对应的头文件通常是gsl/*.h，编译时只需要在gcc命令中添加相应参数即可，可以参考下面两个命令：

?
编译使用GSL库的代码
1
2
gcc `pkg-config --cflags --libs gsl` example.c -o example
gcc -lgsl -lgslcblas -lm example.c -o example

在Windows中使用GSL库要麻烦一些，如果你使用MingW的话，可以到这里下载GSL的库文件。GSL为MingW和Cygwin等环境提供了.a格式的库，使用起来相对还要容易一些，但是如果你使用Virtual C++或者Virtual Studio的话，就要麻烦一些。这里展示一个使用Virtual C++ 6.0的可行的解决方案，如下：

  1. 到http://www6.in.tum.de/~kiss/WinGsl.htm下载WinGsl-Lib-1.4.02.zip，解压到某个目录下面，例如C:\WinGsl；
  2. 打开Virtual C++，点击菜单Tools/Options...，在弹出的对话框里选择Directories选项卡；
  3. 在Show directories for标签下选择Include files，然后在下面的Directories里添加刚刚解压的目录，这里是C:\WinGsl；
  4. 在Show directories for标签下选择Library files，然后在下面的Directories里添加目录C:\WinGsl\Lib；
  5. 复制C:\WinGsl\Bin下的两个文件WinGsl.dll和WinGslD.dll到Virtual C++安装目录里的相应目录，例如C:\Program Files\Microsoft Visual Studio\VC98\Bin；
  6. 建立工程，打开菜单Project/Settings...，在弹出的对话框选择Link选项卡，工程需要用到哪些库里的函数，就把要用到的库文件名添加到Object/library modules下面的文本框里，通常添加文件WinGslLib_s.lib即可。

Erlang分布

Erlang分布是一种连续型概率分布，与指数分布一样多用来表示独立随机事件发生的间隔，Erlang分布不具有马尔科夫性。其概率密度函数如下：

$$f_{\tau_n}(X) = \begin{cases} \frac{\lambda(\lambda X)^{n-1}}{(n-1)!}e^{-\lambda X}, &X>0\cr 0, &X\le0\cr \end{cases}$$

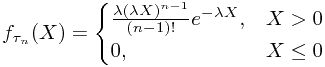
Erlang分布有两个参数，一个是阶数(stage)n，一个是均值(或用)。阶数n=k的Erlang分布称作K-阶Erlang分布。
遵循Erlang分布的随机变量可以分解成多个同参数指数分布的随机变量之和，当阶数n=1时，Erlang分布就退化为指数分布。

此事可以直观理解，柏松过程的两个相邻事件到达时间间隔服从指数分布，而从0时刻直到第n个事件发生的到达时间则服从Erlang分布。

设一柏松过程的到达时间间隔序列为，则若服从参数为的指数分布，到达时间就服从参数为的Erlang分布。

Erlang分布是Gamma分布的特殊情况，Gamma分布的概率密度函数为：

$$f(X) = \begin{cases} \frac{\lambda(\lambda X)^{\alpha-1}}{\Gamma(\alpha)}e^{-\lambda X}, &X>0\cr 0, &X\le0\cr \end{cases}$$

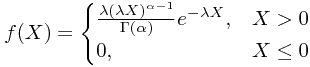
其中Gamma函数可以看作是阶乘的扩展，它有下面的特征(来源)：

$$\begin{cases} \Gamma(\alpha)=(\alpha-1)! &\mbox{if }\alpha\mbox{ is }\mathbb{Z}^+\cr \Gamma(\alpha)=(\alpha-1)\Gamma(\alpha-1) &\mbox{if }\alpha\mbox{ is }\mathbb{Z}^+\cr \Gamma \left( \frac{1}{2} \right) = \sqrt{\pi} \end{cases}$$

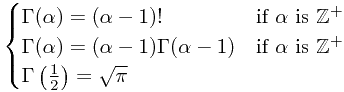
当为整数时，Gamma分布就被称为Erlang分布。后面GSL库中Erlang分布的计算其实就是利用Gamma分布的计算函数进行的。

GSL库产生Erlang分布的随机数

GSL的源代码文件erlang.c中提供了两个关于Erlang分布的函数：

?
erlang.c中的函数
1
2
double gsl_ran_erlang (const gsl_rng * r, const double a, const double n);
double gsl_ran_erlang_pdf (const double x, const double a, const double n);

上述两个函数的参数r为随机数生成器指针，a代表Erlang分布概率密度函数中的，n就是阶数。函数gsl_ran_erlang产生服从Erlang分布的随机数，而gsl_ran_erlang_pdf计算参数为(n,a)的Erlang分布在x处的概率密度。

产生服从Erlang分布的随机数

函数gsl_ran_erlang产生随机数，服从参数为(n, a)的Erlang分布，这个函数产生随机数的基础是r指向的随机数生成器生成的Uniform分布的随机数。在实现上，这个函数将传给它的三个参数原样传给下面的Gamma分布计算函数计算：

?
gamma.c中的函数
1
double gsl_ran_gamma (const gsl_rng * r, const double a, const double n);

gsl_ran_gamma首先确保，如果a<1，则先生成一个(0,1)区间内服从Uniform分布的随机数u，然后返回：

?
1
gsl_ran_gamma (r, 1.0 + a, n) * pow (u, 1.0 / a);

当时，gsl_ran_gamma首先循环调用函数gsl_ran_gaussian_ziggurat，使用Marsaglia-Tsang ziggurat方法产生方差，服从Gaussian分布的随机数x，然后计算，直到为止。

得到满足条件的v以后，计算，然后再产生一个(0,1)区间内服从Uniform分布的随机数u，如果v满足下面两个条件中的任意一个，就接受这个v，否则重复上述生成v的整个过程，直到生成合格的v为止：

$$\begin{cases} u < 1-0.0331x^4, & or \cr ln u < 0.5x^2 + (a-\frac{1}{3})(1-v+ln v) \cr \end{cases}$$

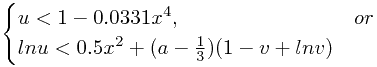
最后，函数返回。

计算概率密度

函数gsl_ran_erlang_pdf计算x处Erlang分布的概率密度，其计算公式为：

$$result = \begin{cases} \frac{exp((n-1)\ln\frac{x}{a}-\frac{n}{a}-lngamma)}{a}, &x>0\cr 0, &x\le0\cr \end{cases}$$

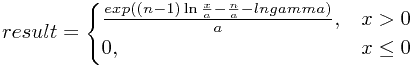
其中lngamma是调用函数gsl_sf_lngamma计算的。其实上式就是由上面Gamma函数的概率密度函数得到的，进行一下简单推导不难验证。

附代码样例：使用GSL库生成Erlang分布的随机数

?
gslErlang.c
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <time.h>
#include <gsl/gsl_rng.h>
#include <gsl/gsl_randist.h>
 
#define MAXRNDNUM 100
  
int main(int argc, char * argv[])
{
    const gsl_rng_type *T; // 随机数生成器类型指针
    gsl_rng *r; // 随机数生成器指针
  
    int i;
    double u; // 随机数变量
 
    const double erlang_a=0.6; // lambda=0.6
    const double erlang_n=2.0; // n=2.0
 
    // gsl_rng_default (gsl_rng_mt19937)
    // gsl_rng_ranlxs0, gsl_rng_ranlxs1, gsl_rng_ranlxs2
    // gsl_rng_ranlxd1, gsl_rng_ranlxd2
    T = gsl_rng_ranlxs0;
 
    gsl_rng_default_seed = ((unsigned long)(time(NULL))); // 取当前时间作为种子
    r = gsl_rng_alloc(T); // 创建随机数生成器实例
 
    for (i=0; i<MAXRNDNUM; i++)
    {
    /** Functions:
     * double gsl_ran_erlang (const gsl_rng * r, const double a, const double n)
     * double gsl_ran_erlang_pdf (const double x, const double a, const double n)
      */
        u = gsl_ran_erlang(r, erlang_a, erlang_n); // 生成服从 Erlang 分布的随机数
        printf("%.5f\n", u);
    }
 
    // 打印 0.0, 1.0 处的概率密度值
    printf("erlang_pdf(0.0)=%.5f\n", gsl_ran_erlang_pdf(0.0, erlang_a, erlang_n));
    printf("erlang_pdf(1.0)=%.5f\n", gsl_ran_erlang_pdf(1.0, erlang_a, erlang_n));
 
    gsl_rng_free(r); // 释放随机数生成器
 
    return 0;
}

使用下面命令编译运行即可：

?
1
2
gcc `pkg-config --cflags --libs gsl` gslErlang.c -o gslErlang
./gslErlang

Tags: gsl erlang distribution gamma distribution random number weibull distribution
Posted in Mathematics | 0 Comments